Synth Basics

8th April, 2018

9 min read

As you may want to create synths using the synth 'framework' I'm working on, I'll run through some of the basics of synthesisers.

Program

A pre-programmed combination of voices and effects, oscillators etc. - synths usually come 'out-of-the-box' with a range of programs that either demonstrate functions of the synth or emulate famous sounds.

Polyphony / monophony - voices and stealing

Synths have a limited number of 'voices' available to play notes. The number of simultaneous voices that can be played is often referred to as the polyphony of a synth.

Early synths were often monophonic meaning they only had one voice available to play a given sound. This meant that if you were already playing a note on one key and hit another key, the note you were playing would be replaced by the new note. You can often choose to have a given program be monophonic for a specific effect.

As mentioned in passing, when a synth is playing as many notes as it can and the player presses another key, the synth will need to 'steal' one of the voices that are currently playing a note. There are a number of ways to do this - take oldest, lowest, or least noticeable.

If the synth implements voice stealing by taking the oldest voice then it will simply reassign the voice that has been playing longest. This could result in a high register note stopping which could be very obvious, so it may be a better idea to take the lowest note and some synths use that as a voice-stealing strategy. Of course, stopping the lowest note might also be very obvious, so there is a more complex strategy that aims to steal a less obvious voice.

Voice doubling

Voices can be doubled to play a note halving the polyphony but enhancing the sound.

Portamento

Portamento means you slide between notes as you play them. In the case of a synthesiser, the portamento setting is the rate at which you change from one note to another. This is not the time taken as that would mean it would take the same time to move between notes spaced far apart as it would between adjacent notes.

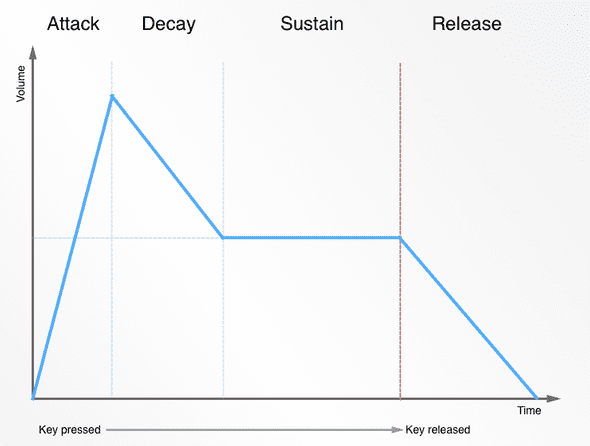
ADSR envelopes - Attack, Decay, Sustain, and Release

This is a key aspect of how a synthesiser will sound. In short, the ADSR envelope determines how quickly the volume of a note increases when the piano key is first hit, how the sound decays away while the key reamins pressed, and finally, how quickly the sound dies away once the key is no longer pressed.

The diagram shows a representation of the volume applied to the note from the moment a piano key is pressed. The attach time is the amount of time it takes for the volume to ramp up from zero to the maximum - which is determined by how hard the piano key was pressed. The sound will then die away until it hits the sustain level, which will be maintained until the key is released. After the key is released the volume will die away to zero according to the release time.

There are both more complex and simpler envelopes, but this ADSR is very common and useful.

Velocity and Polyphonic pressure (or 'Aftertouch')

Pressing a piano key usually transmits the note value and how hard the key was pressed - know as the velocity.

Usually the keyboard only transmits the velocity once, but it is possible for a MIDI keyboard to continue to transmit key pressure while the key is held. If a synthesiser supports it this can be used control various aspects of the note being played such as filters, vibrato etc. The velocity that the keyboard transmits while the key is held is called polyphonic pressure or more commonly aftertouch.

Scales and MIDI notes

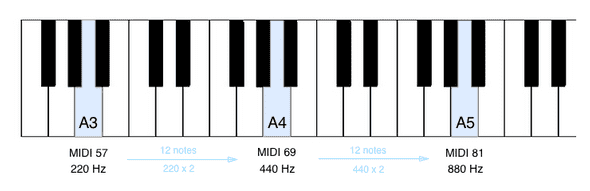
A MIDI keyboard maps each piano key to a value ranging from 0 to 127. A synthesiser must map this to a frequency corresponding to the notes proper position in a particular scale and tuning.

Modern tuning sets A4 (the 'middle' A on a piano keyboard) to be 440 Hz. We can use this to figure out the frequency of every other note on the piano. We'll make some rules first

• an octave is a doubling of frequency
• an octave consists of 12 equally spaced semitones
• we will equate the MIDI note number with semitones

What we're using here is called equal temperament. Lets visualise the relationship between the MIDI notes and the keyboard.

Going from A3 to A4 the frequency increases by 220 Hz, and from A4 to A5 by 440Hz. The frequency doubles each octave, and is also dependent on the position on the keyboard.

The formula we'll use to covert a MIDI note to a frequency is below

// A4 = 440 Hz = MIDI note 69
// where m = MIDI note

const frequency = Math.pow(2, (m - 69) / 12) * 440;

I've tried to outline a basis for understanding how the semitones are related to each other and how the above formula is reached below, if you are interested.

Here comes the science

If we compare the frequency difference between A3 to A4 and then A4 to A5 - we don't use subtraction but division to find the ratio between the notes. It doubles as we said before.

freq A4 / freq A3 = 440 / 220 = 2

freq A5 - freq A4 = 880 / 440 = 2

What about the 12 semitones that make up the octave? The ratio of the frequency of one semitone to the next should be equal. Don't be confused between ratios and differences between the frequency of one semi-tone and the next.

Humans hear octaves as doubling of frequencies and semitones ratios as subdivisions of that, the frequency difference between semitones increases as you play higher up the keyboard, but the ratio remains constant and the notes sound equally spaced to us.

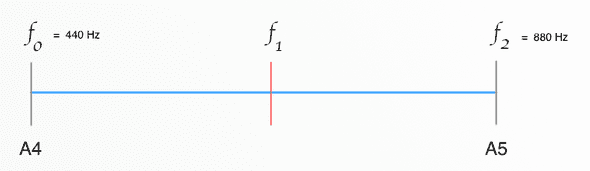
Lets see if we can figure out a system for calculating the note frequencies for each semitone. Lets imagine a simpler octave that only has two semitones, what would be the frequency of our imaginary note f1?

Lets calculate the ratios and see what patterns emerge. Remember the ratios will be the same so we can do some algebra to figure out the value for f1

// we know both ratios should be equal so
f1 / f0 = f2 / f1

// multiply both sides by f1
f1 ^ 2 / f0 = f2

// now multiply both sides by f0
f1 ^ 2 = f0 x f2

// and finally, take the square root of both sides
f1 = sqrt( f0 x f2 )

So plugging in some values

f1 = sqrt(440 x 880) = 622.25 Hz

Great - so we know the frequency of f1 but more importantly we can figure out the expected ratio between semitones

f2 / f1 = 880 / 622.25 = 1.414

f1 / f0 = 622.25 / 440 = 1.414

That figure 1.414 is familiar - it is the square root of 2. The square root is the equivalent of raising 2 to the power of 1 / 2, or in Javascript - Math.pow(2, 1 / 2)

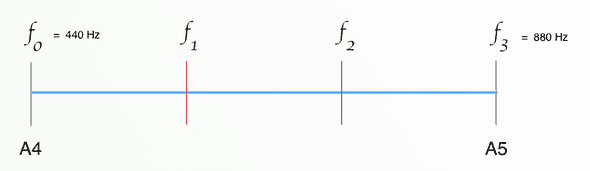
What happens if we have three semitones?

I'm not going to bore you with the details - all simple algebra - but f1 and f2 values are:

f1 = 554.365 Hz

f2 = 698.456 Hz

and when we look at the ratios

f1 / f0 = 554.365 / 440 = 1.2599

f2 / f1 = 698.456 / 554.365 = 1.2599

f3 / f2 = 880 / 698.456 = 1.2599

And that ratio is the cubed root of 2, or raising 2 to the power of 1 / 3 in Javascript - Math.pow(2, 1 / 3) so I think you can see the pattern.

To find the ratio between semitones in any general scale with S semitones

// where S is the number of semitones in an octave

semitone ratio = Math.pow(2, 1 / S)

For our equal temperament scale, the semitone ratio should be

Math.pow(2, 1 / 12) -> 1.0594630943592953

So, given a starting note with a known frequency we can calculate the frequency of other semitones

We could start with any MIDI note as long as we know what frequency it corresponds to. Starting with A4 at 440 Hz what is the frequency of C4 which is 3 semitones higher?

// 3 semitones higher than A4
C4 freq = 440 * Math.pow(2, 3 / 12) = 523.25 Hz

That works, but what about the frequency of C3 which is 9 semitones lower? As it is lower, we just use a negative number -9.

We can just plug in the negative number because raising a number to a negative power will result in a fraction. For instance 2 raised to the power of -1 is 0.5 (or 1 / 2).

// 9 semitones lower than A4
C3 freq = 440 * Math.pow(2, -9 / 12) = 261.626 Hz

So, given that we will be using A4 as the reference point, we will use 440 Hz as the frequency and MIDI note 69 as the reference note, so finally we end up with the formula we started with:

// given 'm' is the MIDI note

frequency = 440 * Math.pow(2, (m - 69) / 12);